Tree
A tree data structure is a hierarchical structure that is used to represent and organize data in a way that is easy to navigate and search. It is a collection of nodes that are connected by edges and has a hierarchical relationship between the nodes. The topmost node of the tree is called the root, and the nodes below it are called the child nodes. Each node can have multiple child nodes, and these child nodes can also have their own child nodes, forming a recursive structure.
This data structure is a specialized method to organize and store data in the computer to be used more effectively. It consists of a central node, structural nodes, and sub-nodes, which are connected via edges. We can also say that tree data structure has roots, branches, and leaves connected with one another.
Why Tree is considered a non-linear data structure?
The data in a tree are not stored in a sequential manner i.e, they are not stored linearly. Instead, they are arranged on multiple levels or we can say it is a hierarchical structure. For this reason, the tree is considered to be a non-linear data structure.
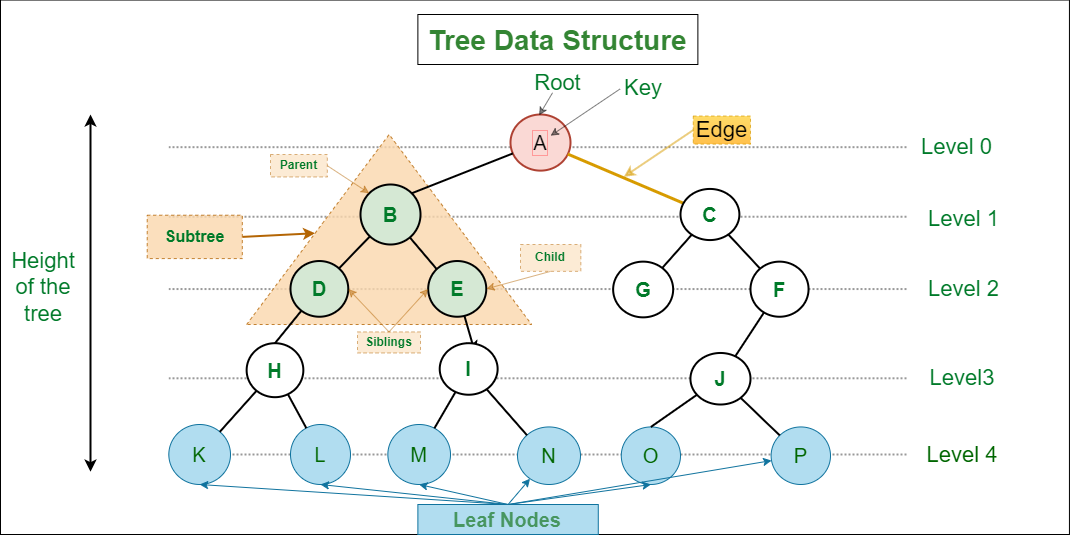
Basic Terminologies In Tree Data Structure:
- Parent Node: The node which is a predecessor of a node is called the parent node of that node. {B} is the parent node of {D, E}.
- Child Node: The node which is the immediate successor of a node is called the child node of that node. Examples: {D, E} are the child nodes of {B}.
- Root Node: The topmost node of a tree or the node which does not have any parent node is called the root node. {A} is the root node of the tree. A non-empty tree must contain exactly one root node and exactly one path from the root to all other nodes of the tree.
- Leaf Node or External Node: The nodes which do not have any child nodes are called leaf nodes. {K, L, M, N, O, P} are the leaf nodes of the tree.
- Ancestor of a Node: Any predecessor nodes on the path of the root to that node are called Ancestors of that node. {A,B} are the ancestor nodes of the node {E}
- Descendant: Any successor node on the path from the leaf node to that node. {E,I} are the descendants of the node {B}.
- Sibling: Children of the same parent node are called siblings. {D,E} are called siblings.
- Level of a node: The count of edges on the path from the root node to that node. The root node has level 0.
- Internal node: A node with at least one child is called Internal Node.
- Neighbour of a Node: Parent or child nodes of that node are called neighbors of that node.
- Subtree: Any node of the tree along with its descendant.
Properties of a Tree:
- Number of edges: An edge can be defined as the connection between two nodes. If a tree has N nodes then it will have (N-1) edges. There is only one path from each node to any other node of the tree.
- Depth of a node: The depth of a node is defined as the length of the path from the root to that node. Each edge adds 1 unit of length to the path. So, it can also be defined as the number of edges in the path from the root of the tree to the node.
- Height of a node: The height of a node can be defined as the length of the longest path from the node to a leaf node of the tree.
- Height of the Tree: The height of a tree is the length of the longest path from the root of the tree to a leaf node of the tree.
- Degree of a Node: The total count of subtrees attached to that node is called the degree of the node. The degree of a leaf node must be 0. The degree of a tree is the maximum degree of a node among all the nodes in the tree.
Some more properties are:
- Traversing in a tree is done by depth first search and breadth first search algorithm.
- It has no loop and no circuit
- It has no self-loop
- Its hierarchical model.
Syntax:
struct Node {
int data;
struct Node *left_child;
struct Node *right_child;
};
Basic Operation Of Tree:
Create – create a tree in data structure.
Insert − Inserts data in a tree.
Search − Searches specific data in a tree to check it is present or not.
Preorder Traversal – perform Traveling a tree in a pre-order manner in data structure (root-> left node -> right node)
In order Traversal – perform Traveling a tree in an in-order manner (left node -> root - > right node)
Post order Traversal –perform Traveling a tree in a post-order manner (left node -> right node -> root)
Binary Tree
What is a Binary Tree?
A binary tree is a tree data structure in which each node can have at most two children, which are referred to as the left child and the right child. The topmost node in a binary tree is called the root, and the bottom-most nodes are called leaves.
Representation of Binary Tree:
Each node in the tree contains the following:
- Data
- Pointer to the left child
- Pointer to the right child
Basic Operations On Binary Tree:
- Inserting an element.
- Removing an element.
- Searching for an element.
- Deletion for an element.
- Traversing an element.
Binary Tree Traversals:
Tree Traversal algorithms can be classified broadly into two categories:
- Depth-First Search (DFS) Algorithms
- Breadth-First Search (BFS) Algorithms
Tree Traversal using Depth-First Search (DFS) algorithm can be further classified into three categories:
- Preorder Traversal (current-left-right): Visit the current node before visiting any nodes inside the left or right subtrees. Here, the traversal is root – left child – right child. It means that the root node is traversed first then its left child and finally the right child.
- Inorder Traversal (left-current-right): Visit the current node after visiting all nodes inside the left subtree but before visiting any node within the right subtree. Here, the traversal is left child – root – right child. It means that the left child is traversed first then its root node and finally the right child.
- Postorder Traversal (left-right-current): Visit the current node after visiting all the nodes of the left and right subtrees. Here, the traversal is left child – right child – root. It means that the left child has traversed first then the right child and finally its root node.
Tree Traversal using Breadth-First Search (BFS) algorithm can be further classified into one category:
- Level Order Traversal: Visit nodes level-by-level and left-to-right fashion at the same level. Here, the traversal is level-wise. It means that the most left child has traversed first and then the other children of the same level from left to right have traversed.
Let us traverse the following tree with all four traversal methods:
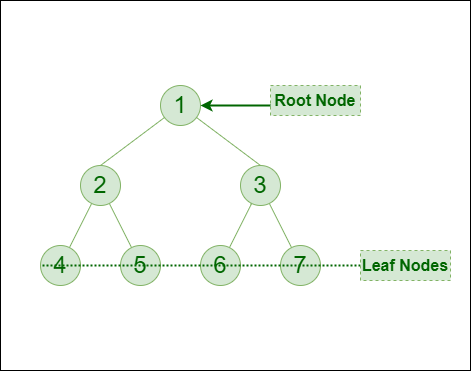
Binary Tree
Pre-order Traversal of the above tree: 1-2-4-5-3-6-7
In-order Traversal of the above tree: 4-2-5-1-6-3-7
Post-order Traversal of the above tree: 4-5-2-6-7-3-1
Level-order Traversal of the above tree: 1-2-3-4-5-6-7
Binary Search Tree(BST)
• A binary search tree (BST) is a binary tree that is either empty or in which every node contains a key (value) and satisfies the following conditions:
• All keys in the left sub-tree of the root are smaller than the key in the root node
• All keys in the right sub-tree of the root are greater than the key in the root node
• The left and right sub-trees of the root are again binary search trees
• A binary search tree is basically a binary tree, and therefore it can be traversed in inorder, preorder and postorder.
• If we traverse a binary search tree in inorder and print the identifiers contained in the nodes of the tree, we get a sorted list of identifiers in ascending order.
• if a current node has no left child, place for insertion has been found;• otherwise, handle the left child with the same algorithm.
• if a current node has no right child, place for insertion has been found;• otherwise, handle the right child with the same algorithm.
Deleting a node from the BST
When we delete a node, three possibilities arise.
1) Node to be deleted is the leaf: Simply remove it from the tree.
50 50
/ \ delete(20) / \
30 70 ———> 30 70
/ \ / \ \ / \
20 40 60 80 40 60 80
2) Node to be deleted has only one child: Copy the child to the node and delete the node.
50 50
/ \ delete(30) / \
30 70 ———> 40 70
\ / \ / \
40 60 80 60 80
3) Node to be deleted has two children: Find inorder successor of the node. Copy contents of the inorder successor to the node and delete the inorder successor.
Note: Inorder predecessor can also be used.
50 60
/ \ delete(50) / \
40 70 ———> 40 70
/ \ \
60 80 80
Note: Inorder successor is needed only when the right child is not empty. In this particular case, in-order successor can be obtained by finding the minimum value in the right child of the node.
Alogirthm for deletion of a node in BST
Follow the below steps to solve the problem:
- If the root is NULL, then return root (Base case)
- If the key is less than the root’s value, then set root->left = deleteNode(root->left, key)
- If the key is greater than the root’s value, then set root->right = deleteNode(root->right, key)
- Else check
- If the root is a leaf node then return null
- else if it has only the left child, then return the left child
- else if it has only the right child, then return the right child
- else set the value of root as of its inorder successor and recur to delete the node with the value of the inorder successor
- Return
Ex: Implementation of binary tree
#include <stdlib.h>
#include <iostream>
using namespace std;
struct node {
int data;
struct node *left;
struct node *right;
};
// New node creation
struct node *newNode(int data) {
struct node *node = (struct node *)malloc(sizeof(struct node));
node->data = data;
node->left = NULL;
node->right = NULL;
return (node);
}
// Traverse Preorder
void traversePreOrder(struct node *temp) {
if (temp != NULL) {
cout << " " << temp->data;
traversePreOrder(temp->left);
traversePreOrder(temp->right);
}
}
// Traverse Inorder
void traverseInOrder(struct node *temp) {
if (temp != NULL) {
traverseInOrder(temp->left);
cout << " " << temp->data;
traverseInOrder(temp->right);
}
}
// Traverse Postorder
void traversePostOrder(struct node *temp) {
if (temp != NULL) {
traversePostOrder(temp->left);
traversePostOrder(temp->right);
cout << " " << temp->data;
}
}
int main() {
struct node *root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(4);
cout << "preorder traversal: ";
traversePreOrder(root);
cout << "\nInorder traversal: ";
traverseInOrder(root);
cout << "\nPostorder traversal: ";
traversePostOrder(root);
}
Ex50: Implementation of a Binary Search Tree
// C++ program to demonstrate delete operation in binary search tree
#include <iostream>
using namespace std;
struct node {
int key;
struct node *left;
struct node *right;
};
// A utility function to create a new BST node
struct node* newNode(int item)
{
struct node* temp = (struct node*)malloc(sizeof(struct node));
temp->key = item;
temp->left = temp->right = NULL;
return temp;
}
// A utility function to do in-order traversal of BST
void inorder(struct node* root)
{
if (root != NULL) {
inorder(root->left);
cout << root->key <<" ";
inorder(root->right);
}
}
/* A utility function to insert a new node with given key in BST */
struct node* insert(struct node* node, int key)
{
/* If the tree is empty, return a new node */
if (node == NULL)
return newNode(key);
/* Otherwise, recur down the tree */
if (key < node->key)
node->left = insert(node->left, key);
else
node->right = insert(node->right, key);
/* return the (unchanged) node pointer */
return node;
}
/* Given a non-empty binary search tree, return the node with minimum key value found in that tree. Note that the entire tree does not need to be searched. */
struct node* minValueNode(struct node* node)
{
struct node* current = node;
/* loop down to find the leftmost leaf */
while ((current && current->left) != NULL)
current = current->left;
return current;
}
/* Given a binary search tree and a key, this function deletes the key and returns the new root */
struct node* deleteNode(struct node* root, int key)
{
// base case
if (root == NULL)
return root;
// If the key to be deleted is smaller than the root's key, then it lies in left subtree
if (key < root->key)
root->left = deleteNode(root->left, key);
// If the key to be deleted is greater than the root's key, then it lies in right subtree
else if (key > root->key)
root->right = deleteNode(root->right, key);
// if key is same as root's key, then This is the node to be deleted
else {
// node has no child
if (root->left == NULL and root->right == NULL)
return NULL;
// node with only one child or no child
else if (root->left == NULL) {
struct node* temp = root->right;
free(root);
return temp;
}
else if (root->right == NULL) {
struct node* temp = root->left;
free(root);
return temp;
}
// node with two children: Get the in-order successor
// (smallest in the right subtree)
struct node* temp = minValueNode(root->right);
// Copy the inorder successor's content to this node
root->key = temp->key;
// Delete the inorder successor
root->right = deleteNode(root->right, temp->key);
}
return root;
}
// Driver Code
int main()
{
/* Let us create following BST
50
/ \
30 70
/ \ / \
20 40 60 80 */
struct node* root = NULL;
root = insert(root, 50);
root = insert(root, 30);
root = insert(root, 20);
root = insert(root, 40);
root = insert(root, 70);
root = insert(root, 60);
root = insert(root, 80);
cout << "Inorder traversal of the given tree \n";
inorder(root);
cout << "\nDelete 20\n";
root = deleteNode(root, 20);
cout << "Inorder traversal of the modified tree \n";
inorder(root);
cout << "\nDelete 30\n";
root = deleteNode(root, 30);
cout << "Inorder traversal of the modified tree \n";
inorder(root);
cout << "\nDelete 50\n";
root = deleteNode(root, 50);
cout << "Inorder traversal of the modified tree \n";
inorder(root);
return 0;
}
2-3 Trees | (Search, Insert and Deletion)
·
Difficulty
Level : Medium
· Last Updated : 05 Sep, 2022
· Read
· Discuss
· Courses
· Practice
· Video
In binary search trees we have
seen the average-case time for operations like search/insert/delete is O(log N)
and the worst-case time is O(N) where N is the number of nodes in the tree.
Like
other Trees include AVL trees, Red Black Tree, B tree, 2-3 Tree is also a height balanced tree.
The time complexity of
search/insert/delete is O(log N) .
A
2-3 tree is a B-tree of order 3.
Properties
of 2-3 tree:
· Nodes with two children are called 2-nodes. The
2-nodes have one data value and two children
· Nodes with three children are called 3-nodes. The
3-nodes have two data values and three children.
· Data is stored in sorted order.
· It is a balanced tree.
· All the leaf nodes are at same level.
· Each node can either be leaf, 2 node, or 3 node.
· Always insertion is done at leaf.
Search: To search a key K in given 2-3 tree T, we follow the following procedure:
Base cases:
1. If T is empty,
return False (key cannot be found in the tree).
2. If current node contains data value which is equal
to K, return True.
3. If we reach the leaf-node and it doesn’t contain
the required key value K, return False.
Recursive Calls:
1. If K <
currentNode.leftVal, we explore the left subtree of the current node.
2. Else if currentNode.leftVal < K < currentNode.rightVal, we explore the middle
subtree of the current node.
3. Else if K >
currentNode.rightVal, we explore the right subtree of the current node.
Consider the following example:




Insertion: There are 3 possible cases in insertion which
have been discussed below:
· Case 1: Insert
in a node with only one data element

· Case 2: Insert
in a node with two data elements whose parent contains only one data
element.



· Case 3: Insert
in a node with two data elements whose parent also contains two data
elements.




In
Deletion Process for a specific value:
· To delete a value, it is replaced by its in-order
successor and then removed.
· If a node is left with less than one data value
then two nodes must be merged together.
· If a node becomes empty after deleting a value, it
is then merged with another node.
To Understand the deletion process-
Consider the 2-3 tree given below

Given 2-3 Tree
delete
the following values from it: 69,72, 99, 81.
To
delete 69, swap it with its in-order
successor, that is, 72. 69 now comes in the leaf node. Remove the value 69 from
the leaf node.

After deletion 69
To
delete 72, 72 is an internal node. To delete
this value swap 72 with its in-order successor 81 so that 72 now becomes a leaf
node. Remove the value 72 from the leaf node.

After deletion 72
Now there is a leaf node that has
less than 1 data value thereby violating the property of a 2-3 tree. So the
node must be merged.
To merge the node, pull down the
lowest data value in the parent’s node and merge it with its left sibling.

Rebalancing to Satisfy 23 Tree
property
To
delete 99, 99 is present in a leaf node, so
the data value can be easily removed.

After deletion 99
Now there is a leaf node that has
less than 1 data value, thereby violating the property of a 2-3 tree.
So the node must be merged. To merge
the node, pull down the lowest data value in the parent’s node and merge it
with its left sibling.

Rebalancing to Satisfy 2-3 Tree
Property
To
delete 81, 81 is an internal node. To delete
this value swap 81 with its in-order successor 90 so that 81 now becomes a leaf
node. Remove the value 81 from the leaf node.

After deletion 81
Now there is a leaf node that has
less than 1 data value, thereby violating the property of a 2-3 tree. So the
node must be merged. To merge the node, pull down the lowest data value in the
parent’s node and merge it with its left sibling.

Rebalancing to Satisfy 2-3 Tree
property
As internal node cannot be empty. So
now pull down the lowest data value from the parent’s node and merge the empty
node with its left sibling

Rebalancing to Satisfy 2-3 Tree
Property
NOTE: In a 2-3 tree, each interior node has either
two or three children. This means that a 2-3 tree is not a binary tree.
Ref: https://www.geeksforgeeks.org/introduction-to-tree-data-structure-and-algorithm-tutorials/
https://www.geeksforgeeks.org/introduction-to-binary-tree-data-structure-and-algorithm-tutorials/?ref=rp
https://www.geeksforgeeks.org/deletion-in-binary-search-tree/
https://www.geeksforgeeks.org/2-3-trees-search-and-insert/