Stacks
A stack is an Abstract Data Type (ADT), commonly used in most programming languages. It is named stack as it behaves like a real-world stack, for example – a deck of cards or a pile of plates, etc.

A real-world stack allows operations at one end only. For example, we can place or remove a card or plate from the top of the stack only. Likewise, Stack ADT allows all data operations at one end only. At any given time, we can only access the top element of a stack.
This feature makes it LIFO data structure. LIFO stands for Last-in-first-out. Here, the element which is placed (inserted or added) last, is accessed first. In stack terminology, insertion operation is called PUSH operation and removal operation is called POP operation.
Stack Representation
The following diagram depicts a stack and its operations −
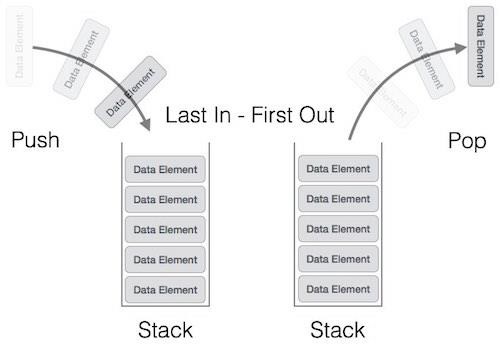
A stack can be implemented by means of Array, Structure, Pointer, and Linked List. Stack can either be a fixed size one or it may have a sense of dynamic resizing. Here, we are going to implement stack using arrays, which makes it a fixed size stack implementation.
Basic Operations
Stack operations may involve initializing the stack, using it and then de-initializing it. Apart from these basic stuffs, a stack is used for the following two primary operations −
push() − Pushing (storing) an element on the stack.
pop() − Removing (accessing) an element from the stack.
When data is PUSHed onto stack.
To use a stack efficiently, we need to check the status of stack as well. For the same purpose, the following functionality is added to stacks −
peek() − get the top data element of the stack, without removing it.
isFull() − check if stack is full.
isEmpty() − check if stack is empty.
At all times, we maintain a pointer to the last PUSHed data on the stack. As this pointer always represents the top of the stack, hence named top. The top pointer provides top value of the stack without actually removing it.
First we should learn about procedures to support stack functions −
peek()
Algorithm of peek() function −
begin procedure peek return stack[top] end procedure
Implementation of peek() function in C programming language −
Example
int peek() { return stack[top]; }
isfull()
Algorithm of isfull() function −
begin procedure isfull if top equals to MAXSIZE return true else return false endif end procedure
Implementation of isfull() function in C programming language −
Example
bool isfull() { if(top == MAXSIZE) return true; else return false; }
isempty()
Algorithm of isempty() function −
begin procedure isempty if top less than 1 return true else return false endif end procedure
Implementation of isempty() function in C programming language is slightly different. We initialize top at -1, as the index in array starts from 0. So we check if the top is below zero or -1 to determine if the stack is empty. Here's the code −
Example
bool isempty() { if(top == -1) return true; else return false; }
Push Operation
The process of putting a new data element onto stack is known as a Push Operation. Push operation involves a series of steps −
Step 1 − Checks if the stack is full.
Step 2 − If the stack is full, produces an error and exit.
Step 3 − If the stack is not full, increments top to point next empty space.
Step 4 − Adds data element to the stack location, where top is pointing.
Step 5 − Returns success.
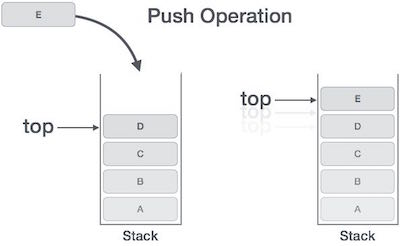
If the linked list is used to implement the stack, then in step 3, we need to allocate space dynamically.
Algorithm for PUSH Operation
A simple algorithm for Push operation can be derived as follows −
begin procedure push: stack, data if stack is full return null endif top ← top + 1 stack[top] ← data end procedure
Implementation of this algorithm in C, is very easy. See the following code −
Example
void push(int data) { if(!isFull()) { top = top + 1; stack[top] = data; } else { printf("Could not insert data, Stack is full.\n"); } }
Pop Operation
Accessing the content while removing it from the stack, is known as a Pop Operation. In an array implementation of pop() operation, the data element is not actually removed, instead top is decremented to a lower position in the stack to point to the next value. But in linked-list implementation, pop() actually removes data element and deallocates memory space.
A Pop operation may involve the following steps −
Step 1 − Checks if the stack is empty.
Step 2 − If the stack is empty, produces an error and exit.
Step 3 − If the stack is not empty, accesses the data element at which top is pointing.
Step 4 − Decreases the value of top by 1.
Step 5 − Returns success.
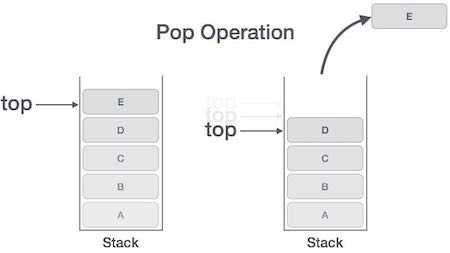
Algorithm for Pop Operation
A simple algorithm for Pop operation can be derived as follows −
begin procedure pop: stack
if stack is empty return null endif data ← stack[top] top ← top - 1 return data end procedure
Ex: Implement stack as Array
// Implementing stack with arrays
#include <iostream>
#define ssize 10
using namespace std;
class stack{
int ary[ssize];
int top;
public:
stack() {
top = -1;
}
void push(int val){
if (top <= ssize - 1) {
top++;
ary[top] = val;
}
else cout << "Stack already Full";
}
void pop(){
if (top>= 0){
cout << "Popped out value is = " << ary[top] << endl;
top--;
}
else cout << " Stack is emplty";
}
void display(){
cout << "Stack values are : " << endl;
for (int i=top;i>=0;i--){
cout << ary[i] << endl;
}
}
};
int main(){
stack s1;
int val, choice;
while (1) {
cout << "Enter 1 for push, 2 for pull, 3 for display and 4 for exit " << endl;
cin >> choice;
switch (choice)
case 1: cout << "Enter value to be pushed : " << endl;
cin >> val;
s1.push(val);
break;
case 2: s1.pop(); break;
case 3: s1.display(); break;
case 4: exit(-1);
}
return 0;
}
Implement a stack data structure using two queues.
In a stack, we add elements in LIFO (Last In, First Out) order. This means that the last element inserted in the stack will be the first one removed. The basic operations of a stack are:
- push — insert an element at the top
- pop — remove an element from the top
In a queue, we add elements in FIFO (First In, First Out) order, meaning that the first element inserted is the first one to be removed. The basic operations of the queue are:
- enqueue — insert an element at the rear
- dequeue — remove an element from the front
queue provides the functionality of a queue data structure.In order to create a queue in C++, we first need to include the queue header file.
#include <queue>Once we import this file, we can create a queue using the following syntax:
queue<type> q;Here, type indicates the data type we want to store in the queue. For example,
// create a queue of integer data type
queue<int> integer_queue;
// create a queue of string data type
queue<string> string_queue;
In C++, the queue class provides various methods to perform different operations on a queue.
Methods Description push()inserts an element at the back of the queue pop()removes an element from the front of the queue front()returns the first element of the queue back()returns the last element of the queue size()returns the number of elements in the queue empty()returns true if the queue is empty
- push (E element)
- if q1 is empty, enqueue E to q1
- if q1 is not empty, enqueue all elements from q1 to q2, then enqueue E to q1, and enqueue all elements from q2 back to q1
- pop
- dequeue an element from q1
As we see, q1 acts as the main source for the stack, while q2 is just a helper queue that we use to preserve the order expected by the stack.
/* Program to implement a stack using two queue */
#include <iostream>
using namespace std;
class Stack {
// Two inbuilt queues
queue<int> q1, q2;
public:
void push(int x)
{
// Push x first in empty q2
q2.push(x);
// Push all the remaining elements in q1 to q2.
while (!q1.empty()) {
q2.push(q1.front());
q1.pop();
}
// swap the names of two queues
queue<int> q = q1;
q1 = q2;
q2 = q;
}
void pop()
{
// if no elements are there in q1
if (q1.empty())
return;
else
q1.pop();
}
int top()
{
if (q1.empty())
return -1;
else
return q1.front();
}
int size() { return q1.size(); }
};
// Driver code
int main()
{
Stack s;
s.push(1);
s.push(2);
s.push(3);
cout << "current size: " << s.size() << endl;
cout << s.top() << endl;
s.pop();
cout << s.top() << endl;
s.pop();
cout << s.top() << endl;
cout << "current size: " << s.size() << endl;
return 0;
}